t_kahi’s blog

KNIMEやCellProfiler、創薬に関する記事と，日々のメモです

【KNIME】One-way ANOVA（対応なし/対応あり）の結果を出力する

KNIME

こんにちは，@PKです.

一元配置分散分析（One-way ANOVA）は１つの要因によって影響を受ける3群間以上の平均の差を検定する統計的手法です．
一元配置分散分析 - Wikipedia
One-way ANOVAで有意差有り⇒多重検定という流れで使用されます．
このOne-way ANOVAには，対応がないものと，対応があるもの（同じ集団に対してサンプリングしたもの）があります．
今回はKNIMEでOne-way ANOVA（対応なし/対応あり）それぞれの結果を出力します．

用いたサンプルデータなどはこちらのサイトを参考にさせて頂きました．
データ解析・マイニングとR言語

KNIME Workflow

KNIME Workflowは以下の通りです．
f:id:t_kahi:20190616001813p:plain
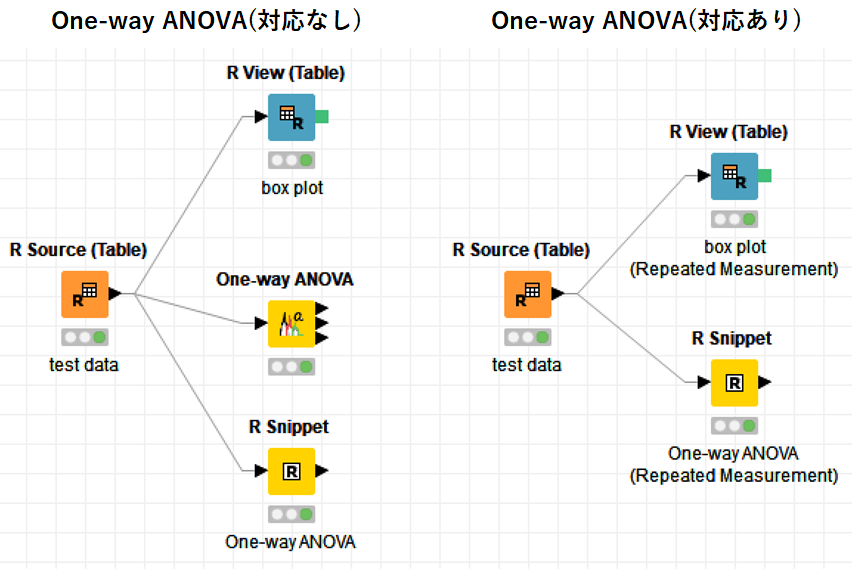
One-way ANOVA対応なし・対応ありそれぞれのサンプルデータに対して，でBox Plotによるデータの表示とOne-way ANOVAを実施しています．

対応のないOne-way ANOVAについては専用のノードが用意されています．
nodepit.com
中身を理解するために，「R snippet 」ノードでも同じ処理を行ってみました．
一方で，対応のあるOne-way ANOVAは専用ノードが無いため，「R snippet」のみでデータ解析を行いました．

One-way ANOVA（対応なし）

f:id:t_kahi:20190616082434p:plain

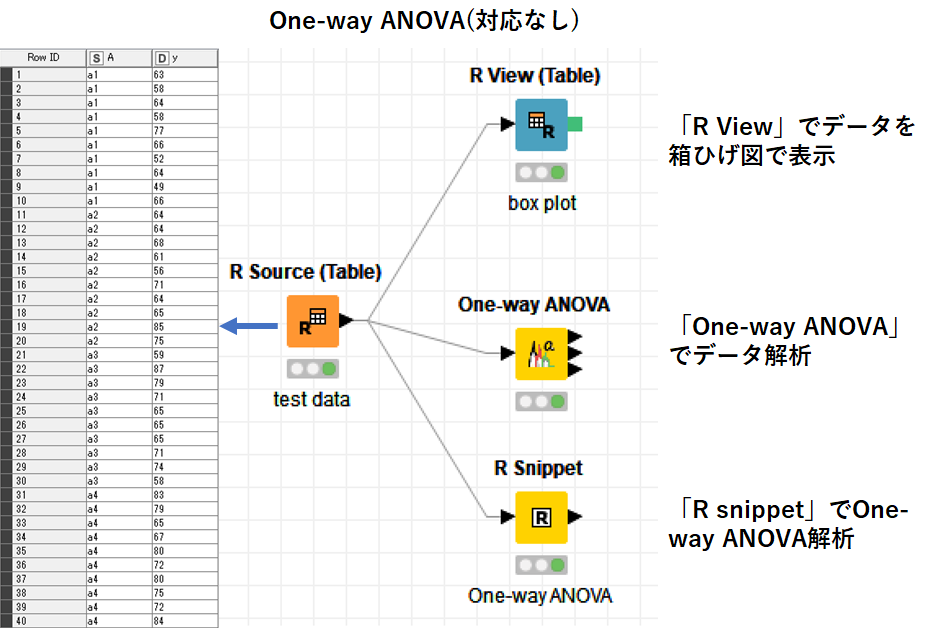
まず．サンプルデータを「R source」で入力します．

#R source
a1<- c(63,58,64,58,77,66,52,64,49,66) 
a2<- c(64,64,68,61,56,71,64,65,85,75) 
a3<- c(59,87,79,71,65,65,65,71,74,58) 
a4<- c(83,79,65,67,80,72,80,75,72,84) 

data<- data.frame(A=factor(c(rep("a1",10),rep("a2",10),rep("a3",10),rep("a4",10))),y=c(a1,a2,a3,a4)) 

knime.out <- data

出力結果は上図の通りになります．カラムAに各グループ(a1~a4) ，カラムyにデータが入っています．

続いて，前回紹介しましたが，「R View」でデータを箱ひげ図で表示します．
【KNIME】箱ひげ図(box plot)を作成する：「Conditional box plot」 VS 「R view」 - t_kahi’s blog

#R View
library(ggplot2)
ggplot(knime.in, aes(x = A, y = y, color = A)) + #初期設定
  geom_boxplot() +  #boxplotを指定
  geom_jitter() +   #分布を重ねる
  labs(x = "group",
       y = "results") + #データのラベルを付ける
         theme(axis.text=element_text(size=12),
        axis.title=element_text(size=14,face="bold")) #データの文字サイズを変える

それぞれのグループ間で色を変えて表示してあります．
データの平均値はa1⇒a2⇒a3⇒a4と高くなっていることがわかります．
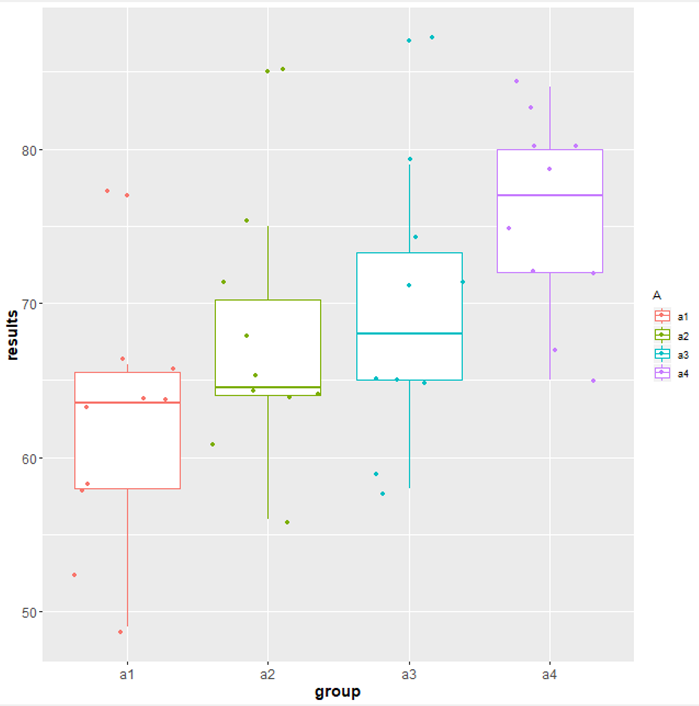f:id:t_kahi:20190615101630p:plain これら４群の平均値に差があるかどうかをone-way ANOVAで解析します．

まずは「One-way ANOVA」ノードを使用します．
設定画面から，「Grouping Column」をAに，「Test Columns」をyにします．また，信頼区間は95%にします．
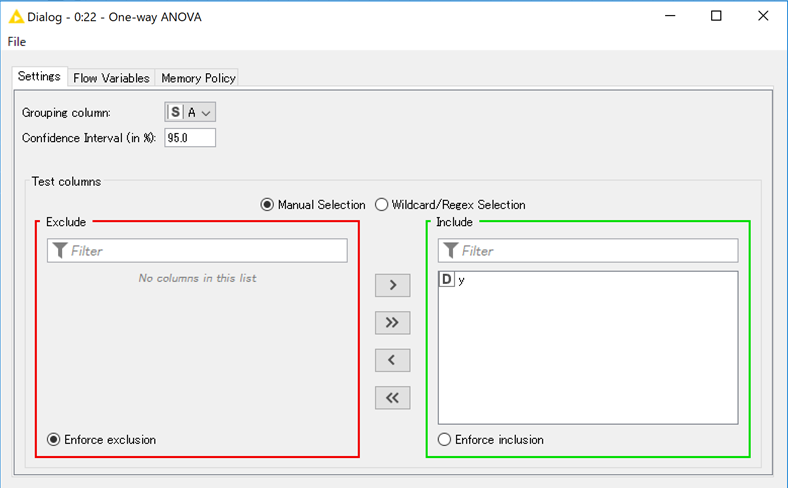f:id:t_kahi:20190616083757p:plain ノードを実行すると，「One-way ANOVA」はそれぞれのポートから３つの結果(One-way ANOVA結果，Leveneテスト，各群の統計値）を返します．
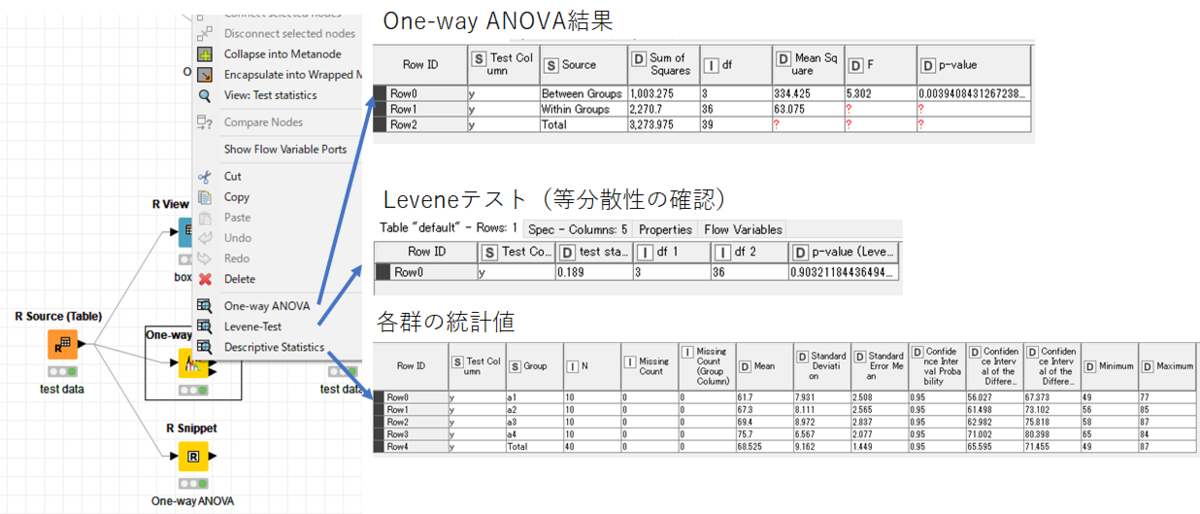f:id:t_kahi:20190616085125p:plain One-way ANOVA結果から，群間のp値は0.00394ということで，4群の平均値は有意に差があることがわかります．

確認のため同じ事を「R snippet」で実行します．

#R snippet
results <- aov(y~A, knime.in)
sum_test = unlist(summary(results))#リストをばらばらにする
names(sum_test)#要素の確認
sum_test["Df1"]#ベクトルなので$で列の情報が取れないので，["Df1"]とした
Df <- c(sum_test["Df1"],sum_test["Df2"])
P.value <- c(sum_test["Pr(>F)1"],sum_test["Pr(>F)2"])
Mean_Sq <- c(sum_test["Mean Sq1"],sum_test["Mean Sq2"])
Sum_Sq <- c(sum_test["Sum Sq1"],sum_test["Sum Sq2"])
F_value <- c(sum_test["F value1"],sum_test["F value2"])
knime.out <- data.frame(Sum_Sq,Df,Mean_Sq,F_value,P.value)

Summaryデータを取得するのは簡単なのですが，取得したデータをポートに出力する部分で少し手間取りました．
データ形式を理解できていないからなのですが，listやdata.frameだと，$を使えば列を抜き出せるのに，ベクトルだとできないらしい…
r - Extract p-value from aov - Stack Overflow
上の回答を参考にしました．
結果を出力すると，「One-way ANOVA」ノードの結果と同様に群間比較のF統計量やP値が返ってきます．

One-way ANOVA（対応あり）

f:id:t_kahi:20190616090609p:plain

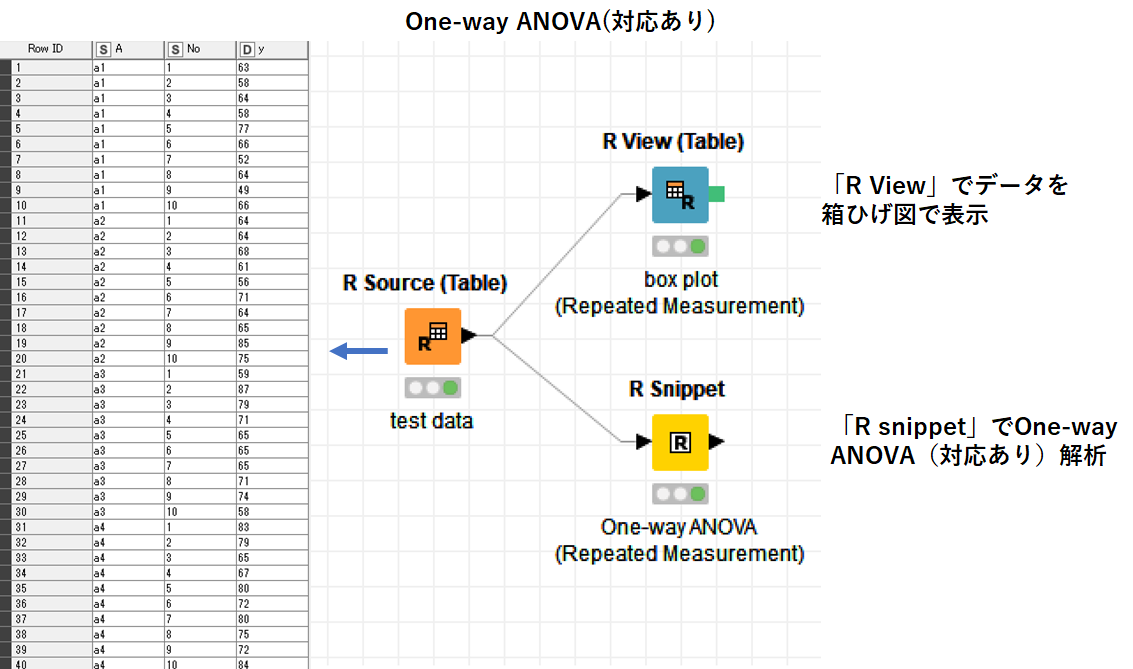
続いて，One-way ANOVA（対応あり）について考えます．
サンプルデータを「R Source」で作成します．

#R Source
a1<- c(63,58,64,58,77,66,52,64,49,66) 
a2<- c(64,64,68,61,56,71,64,65,85,75) 
a3<- c(59,87,79,71,65,65,65,71,74,58) 
a4<- c(83,79,65,67,80,72,80,75,72,84) 

data<-data.frame(A= factor(c(rep("a1",10), rep("a2",10), rep("a3",10), rep("a4",10))),No= factor(rep(1:10, 4)),y=c(a1,a2,a3,a4)) 

knime.out <- data

上図に示す通り，先ほどと同じデータに新しくNoというカラムが追加され，それぞれの対応する行ごとに番号が振られています．
先ほどのデータは，a1~a4という異なる因子条件Aの下でn=10の平均値の比較を行いましたが，今度はNo.1~10の独立したサンプルにおいて，a1~4の因子条件Aで測定した際に因子間・あるいはサンプル間で差があるかどうかを検定します．

#R View
library(ggplot2)
ggplot(knime.in, aes(x = A, y = y)) +
  geom_boxplot(aes(group=A)) + #boxplot(goup=A)を指定
  geom_jitter(aes(color=No)) + #分布を重ねる(color=No)
  labs(x = "group",
       y = "results") + #データのラベルを付ける
  theme(axis.text=element_text(size=12),
        axis.title=element_text(size=14,face="bold"))

それぞれのグループ間で色を変えて表示してありましたが，今度はNoごとに色を変えて表示しています． f:id:t_kahi:20190616091408p:plain

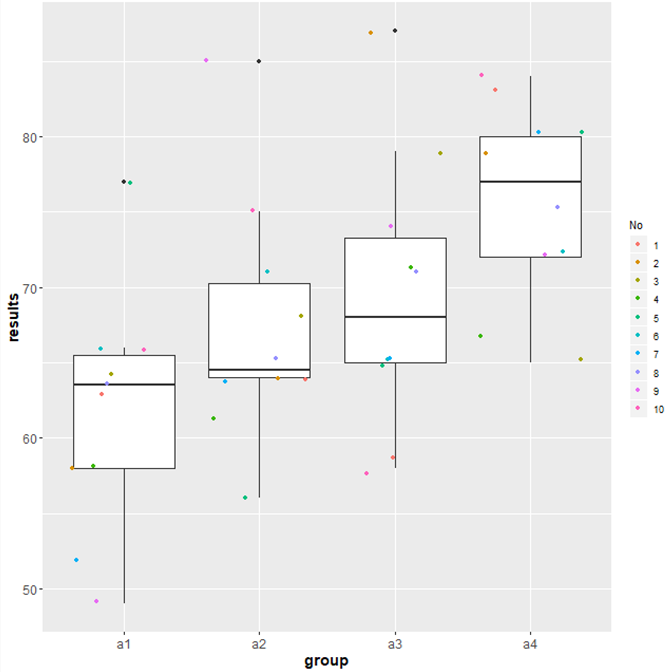
これら対応がある場合のOne-way ANOVAはKNIMEノードが無いため，「R snippet」で処理する必要があるようです．

#R snippet
results <- aov(y~A+No, knime.in) #Noの情報を加えてANOVA
sum_test = unlist(summary(results))#リストをばらばらにする
names(sum_test)#要素の確認
sum_test["Df1"]#ベクトルなので$で列の情報が取れないので，["Df1"]とした
sum_test["Df2"]
sum_test["Pr(>F)1"]
sum_test["Pr(>F)2"]
Df <- c(sum_test["Df1"],sum_test["Df2"],sum_test["Df3"])
P.value <- c(sum_test["Pr(>F)1"],sum_test["Pr(>F)2"],sum_test["Pr(>F)3"])
Mean_Sq <- c(sum_test["Mean Sq1"],sum_test["Mean Sq2"],sum_test["Mean Sq3"])
Sum_Sq <- c(sum_test["Sum Sq1"],sum_test["Sum Sq2"],sum_test["Sum Sq3"])
F_value <- c(sum_test["F value1"],sum_test["F value2"],sum_test["F value3"])
knime.out <- data.frame(Sum_Sq,Df,Mean_Sq,F_value,P.value)

結果を以下に示します．
1行目が群間比較，2行目が各No間比較をしています．

4群間を比較したp値は0.012なので，要因Aの4群間の平均値の差はありそうです．
しかしNoでの比較についてはp値は0.97ということで有意な差はないという結果になりました．

まとめ

One-way ANOVA（対応なし/対応あり）の結果をKNIMEの「One-way ANOVA」ノードと，「R snippet」それぞれで行いました．
Rについては，データ解析よりも，データをきちんと出力できる形に変換することのほうがやはり難しかったです．

余談ですが，「One-way ANOVA⇒有意差あり⇒多重検定」というのは少し強引な言い方で，多重検定の種類によってはOne-way ANOVAが必要ないものもあります．
One-way ANOVAをどのように使うかについては，下記資料がわかりやすかったです．
https://www.jstage.jst.go.jp/article/kagakutoseibutsu/51/7/51_483/_pdf
私のための統計処理 ー多重比較検定
Dunnet法，Tukey‒Kramer法などはF統計量を用いないので，ANOVAを行う必要は無いようです．