Comparison of diversity index (Quadratic entropy, Shannon entropy & Simpson index)

I posted blog about calculation of Quadratic Entropy (QE) before.

Today, I will calculate and compare the diversity indices, Quadratic Entropy (QE), Shannon Entropy & Simpson index.

these diversity indices were used to evaluate tumor cell diversity. Evaluating tumor heterogeneity in immunohistochemistry-stained breast cancer tissue | Laboratory Investigation

f:id:t_kahi:20190824150814p:plain

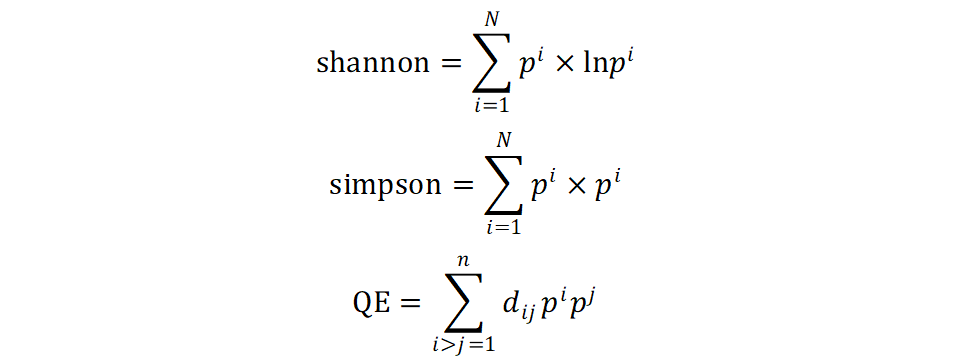
I calculate Quadratic Entropy (QE), Shannon Entropy & Simpson index for the same as the previous post.

library(ggplot2)

min <- 0
max <- 20

hist1 <- rnorm(500,10,1)
hist2 <- rnorm(500,10,1)
hist <- c(hist1, hist2)
data <- data.frame(intensity = hist)
head(data)

len <- length(data$intensity)
K <- 1 + log2(len)

plt <- ggplot(data,aes(x=intensity))+
  geom_histogram(bins=round(K))

plt

add <- max/K

break_data <- seq(min, max, add)
break_data <- c(break_data, break_data[length(break_data)]+add)
data$bins <- cut(data$intensity, breaks=break_data,label=FALSE)

data <- na.omit(data)
hist_data <- data.frame(table(data$bins))

result <- data.frame(Num = seq(1:length(break_data)))
result <- merge(result,hist_data,by.x="Num", by.y ="Var1",all=T)
result[is.na(result)] <- 0

result$"Freq" <- result$"Freq"/sum(result$"Freq")
result$"Num" <- (result$"Num"-min(result$"Num"))/(max(result$"Num")-min(result$"Num"))

distance <-  dist(result$"Num",method = "euclidean")

D <- as.matrix(distance)
p <- as.vector(result$"Freq")

#Calculate Quadratic Entropy
QE <- c(crossprod(p, D %*% p)) / 2
QE

#Calculate Shannon Entropy
shanon <- -sum(result$"Freq"*log2(result$"Freq"+1e-15) )
shanon

#Calculate Simpson idex
simp <- sum(result$"Freq"*result$"Freq" )
simp

I tested multiple histogram which changed rnorm mean values and number of datasets.

The following data is the calculation result of QE, Shannon entropy and Simpson index.
The 50 : 50 mix consists of 2 units normal distribution, and the mean of the distribution is changed as follows:
f:id:t_kahi:20190824163410p:plain
These data showed that the value of QE are increased when distribution of histogram were separated.

Next, the following data is the calculation result of different 10∶1 mix which consists of 2 unit normal distributions.
f:id:t_kahi:20190824163427p:plain
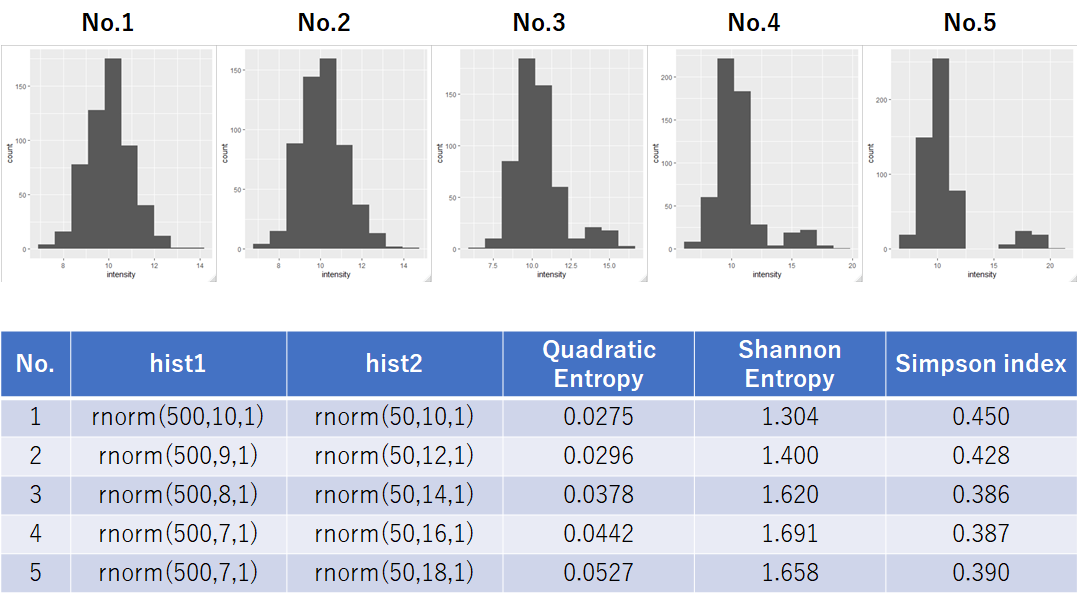
Shannon entropy and Simpson index are not sensitive to a small 10% subpopulation. On the other hand, it is shown that the value of QE increased steadily.